What's a seed phrase?
 Contents
Contents
- Introduction
- Keys
- Mnemonic Code and Seed generation
- Security
- Derivation paths and key identifiers
Introduction
Also known as a mnemonic or mnemonic code, if you have ever used a
bitcoin wallet you will likely have come across a seed phrase when
setting up or backing up your wallet, you will have been asked to write
down 12 or 24 random words. It is essential that you
back this up offline (either on paper or steel) and
keep it private, it is used to generate all of your
bitcoin private keys and anyone who knows your seed can spend your
bitcoin. This is a unique property of bitcoin, knowing is owning,
or put more poetically
the map is the territory.
For most people, this is all you need to know. This post will go into
more of the details behind hierarchical deterministic wallets (often
referred to as hd wallets). For more information see
bip32 Hierarchical Deterministic Wallets,
bip39 Mnemonic code for generating deterministic keys
and the book
Mastering Bitcoin
by Andreas M.Antonopoulos.
Keys
Put simply, public keys are used to receive bitcoin while private keys
are used to send bitcoin. For more information see
ECDSA.
Legend
-
A red arrow represents a process which
cannot be reversed other than by means of brute force
-
Data in a blue box may give someone
access to coins

Mnemonic Code and Seed generation
For the case of a 24 word mnemonic, 256 bits of entropy are generated by
either your computer, a hardware wallet or
manually
(by dice or other means) i.e. a number between 1 and 2256
≈ 1077 is chosen at random, for reference it is
estimated
that there are between 1078 and 1082 atoms in the
observable universe. By the processes displayed below this entropy is
used to derive a seed which inturn derives everyone of your key pairs
i.e. anyone with knowledge of this entropy can spend your bitcoin, for
this reason it is very important that this entropy is generated securely
and that it really is random - something which can be hard to prove.
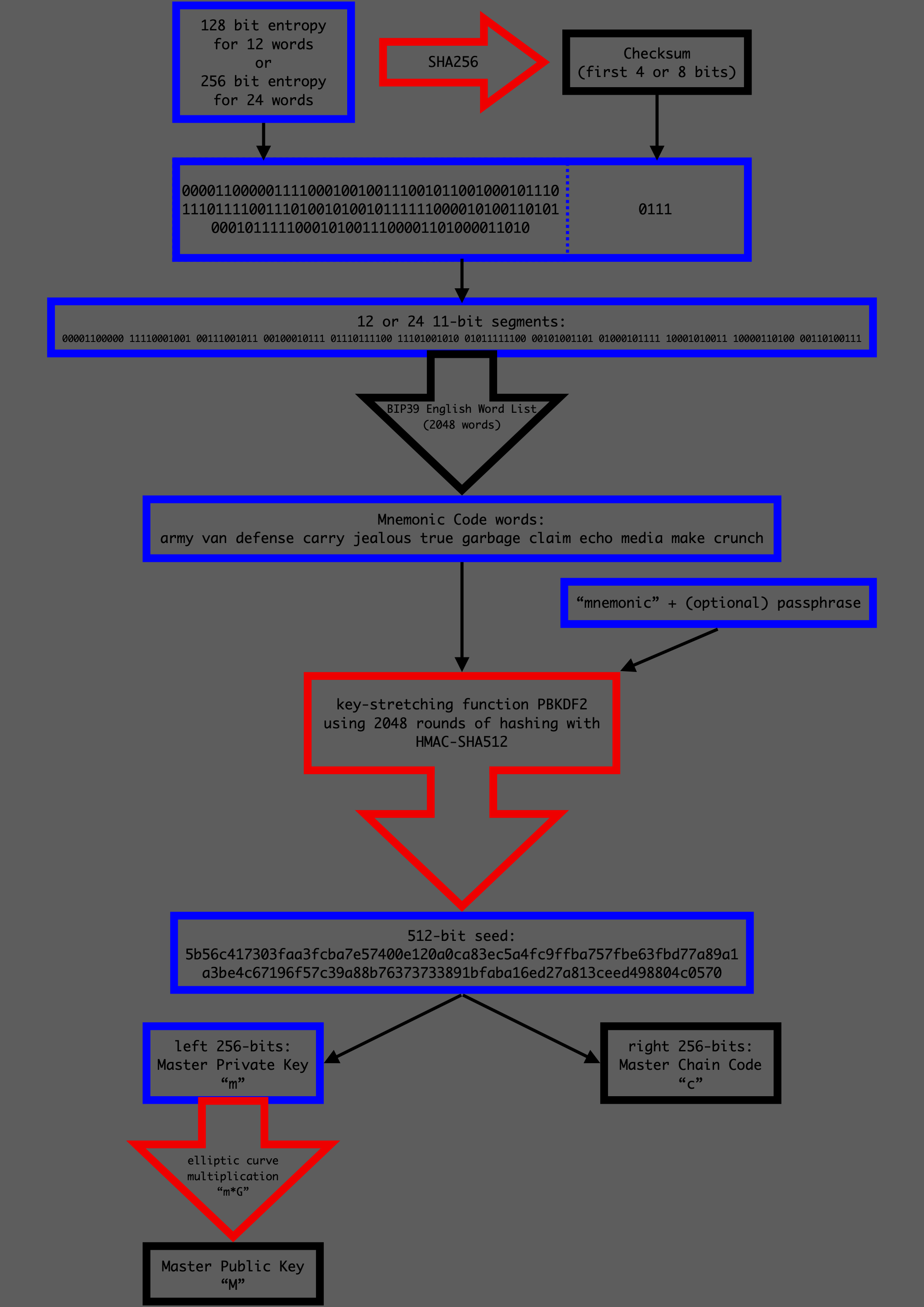
The optional passphrase gives the user the ability to add an extra
factor by requiring a passphrase in addition to the mnemonic code.
Adding a passphrase will result in an entirely different seed, this is
an excellent option if you do not trust your hardware's random number
generator, however it adds complexity to your backup process.
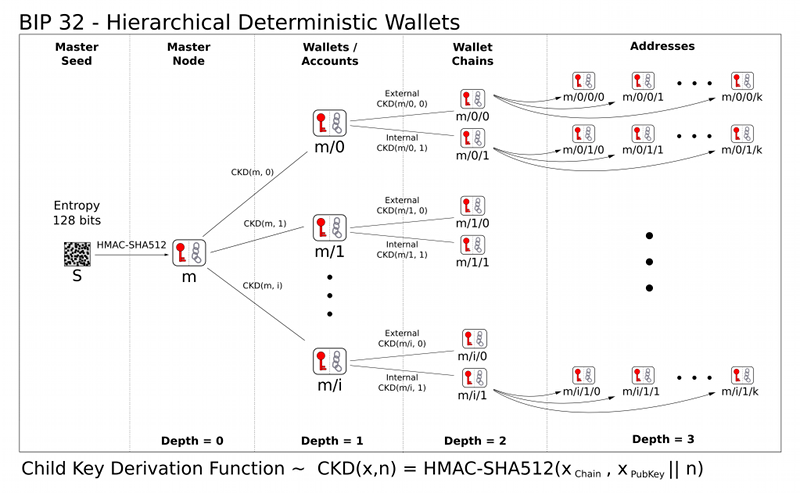
Child key derivation
Any key (public or private) can be combined with the chain code to form
a 512-bit extended key (prefix: xpub or xpriv) which can be used to
derive "child keys". An extended public key (a public key combined with
the chain code) can derive all child public keys
only, whereas extended private keys can derive child private keys
which can in turn be used to derive their corresponding public keys.
This is a great security feature, a web-store can keep an extended
public key on an online computer for receiving payments (without having
to reuse a single bitcoin address) while the corresponding extended
private key is kept securely offline.
Each extended key has 232 (about 4 billion) child keys, which
are derived by the process described in the diagram below. Half of these
child keys are hardened, these keys have a security benefit which will
be explained below but come with the inconvenience that parent extended
public keys cannot derive their hardened child public keys, these must
be derived using the parent extended private key to derive the child
private key and then use elliptic curve multiplication to get the
corresponding child public key. If the index number is between 0 and
231-1 the child key is normal, otherwise it is hardened. The
derivation process for hardened keys is very similar, only the parent
private key is used in place of the parent public key (see
orange arrow).
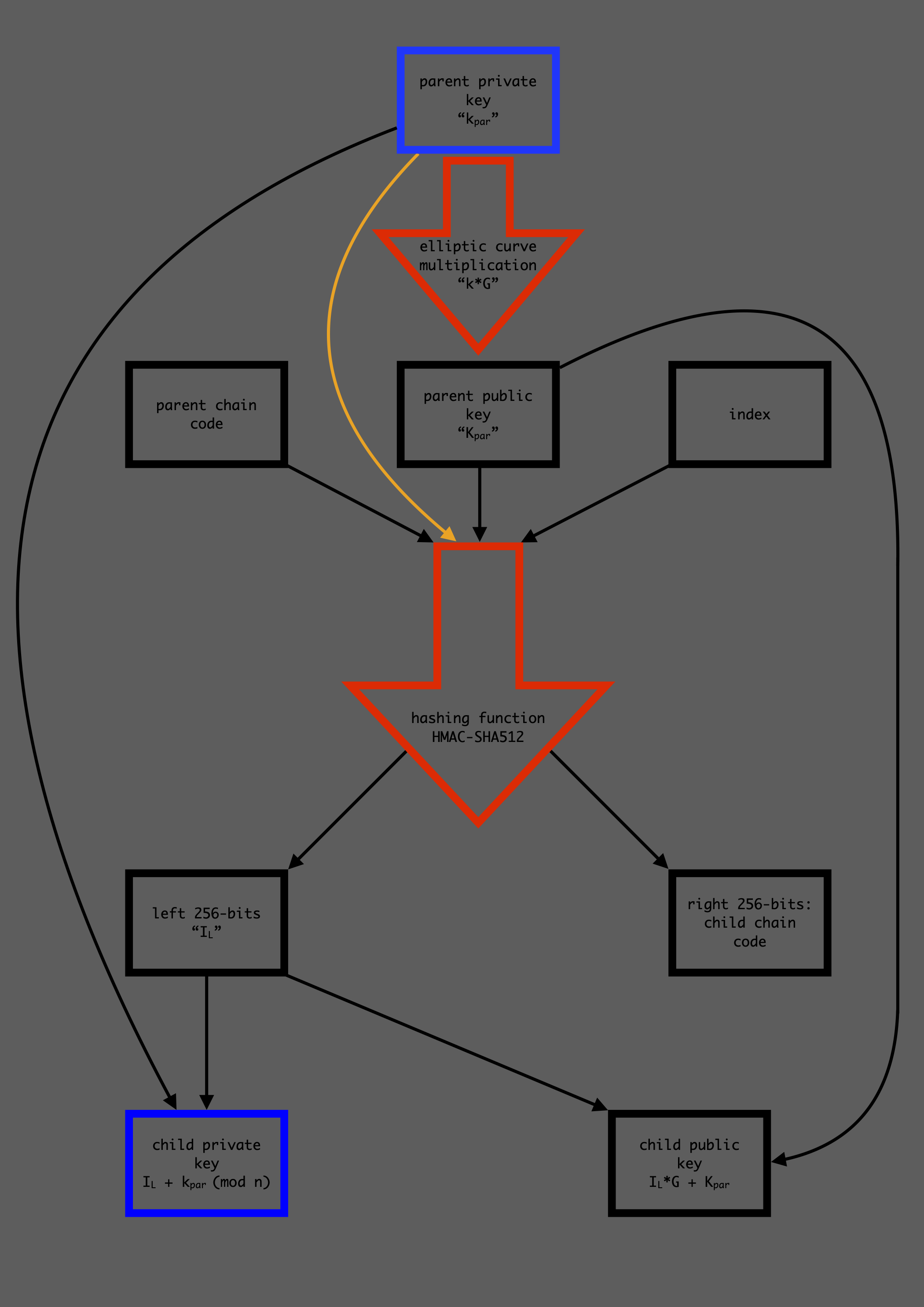
Because elliptic curve multiplication is distributive the child public
key (Ki) derived from the non-hardened child private key
(ki) is equal to the child public key derived from the parent
extended public key: Ki = ki*G = (IL +
kpar)*G = IL*G + kpar*G =
IL*G + Kpar.
Security
-
Given a public key, you cannot find the corresponding private key more
efficiently than by solving the
EC discrete logarithm problem
(assumed to require 2128 group operations).
-
Given a child private key, chain code and index, an attacker cannot
find the parent private key more efficiently than a 2256
brute force of HMAC-SHA512.
-
Given any number of child private keys, their chain codes and indexes
you cannot determine whether they are derived from a common parent key
more efficiently than a 2256 brute force of HMAC-SHA512.
-
Given a parent extended public key and a child public key it is not
hard to find its index.
-
Given a parent extended public key and a non-hardened child private
key,
it is not hard to find the parent private key. This
is the reason for using hardened child keys.
Derivation paths and key identifiers
By the processes described above an endless family tree of keys can be
derived from a human readable mnemonic code which is easy enough to
remember. This is very useful for segregating funds for say different
parts of a business, each department can have it's own branch of the
tree, but because this tree has so many branches it is worth backing up
the derivation path of the extended keys you use to derive receiving
addresses as well as using standard derivation paths,
failure to do so could result in loss of funds.
m / purpose' / coin type' / account' / change / address index
(i' is used to represent the ith hardened child istead of
i+231 for ease of notation.)
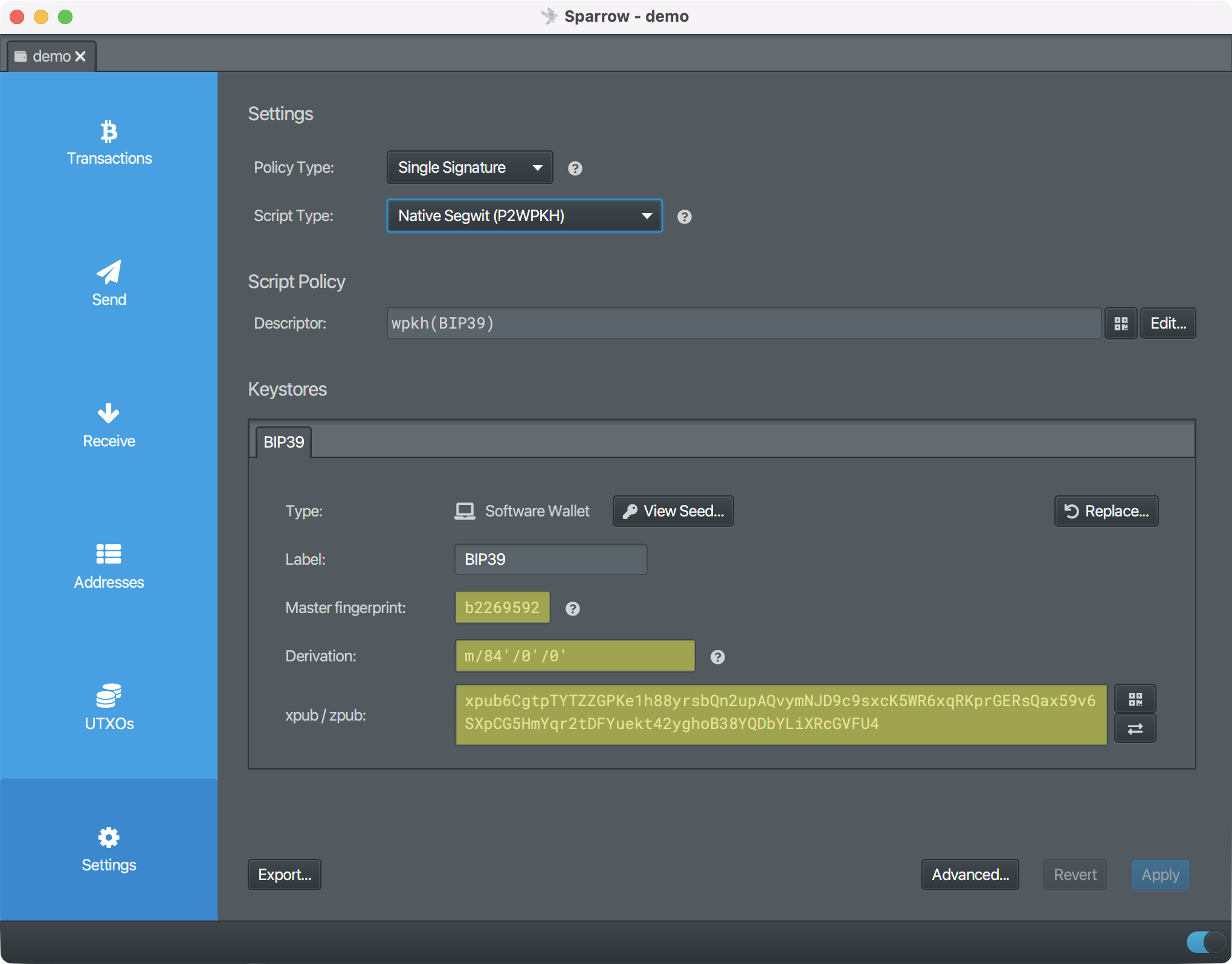
In the example above (using
Sparrow wallet) the extended public key (xpub) is the 0th hardened child
of the 0th hardened child of the 84th hardened
child of the master key. This is a standard derivation defined in
bip84. The master fingerprint is just the first 32-bits of the Hash160 of
the public key and is used to quickly identify different keys.
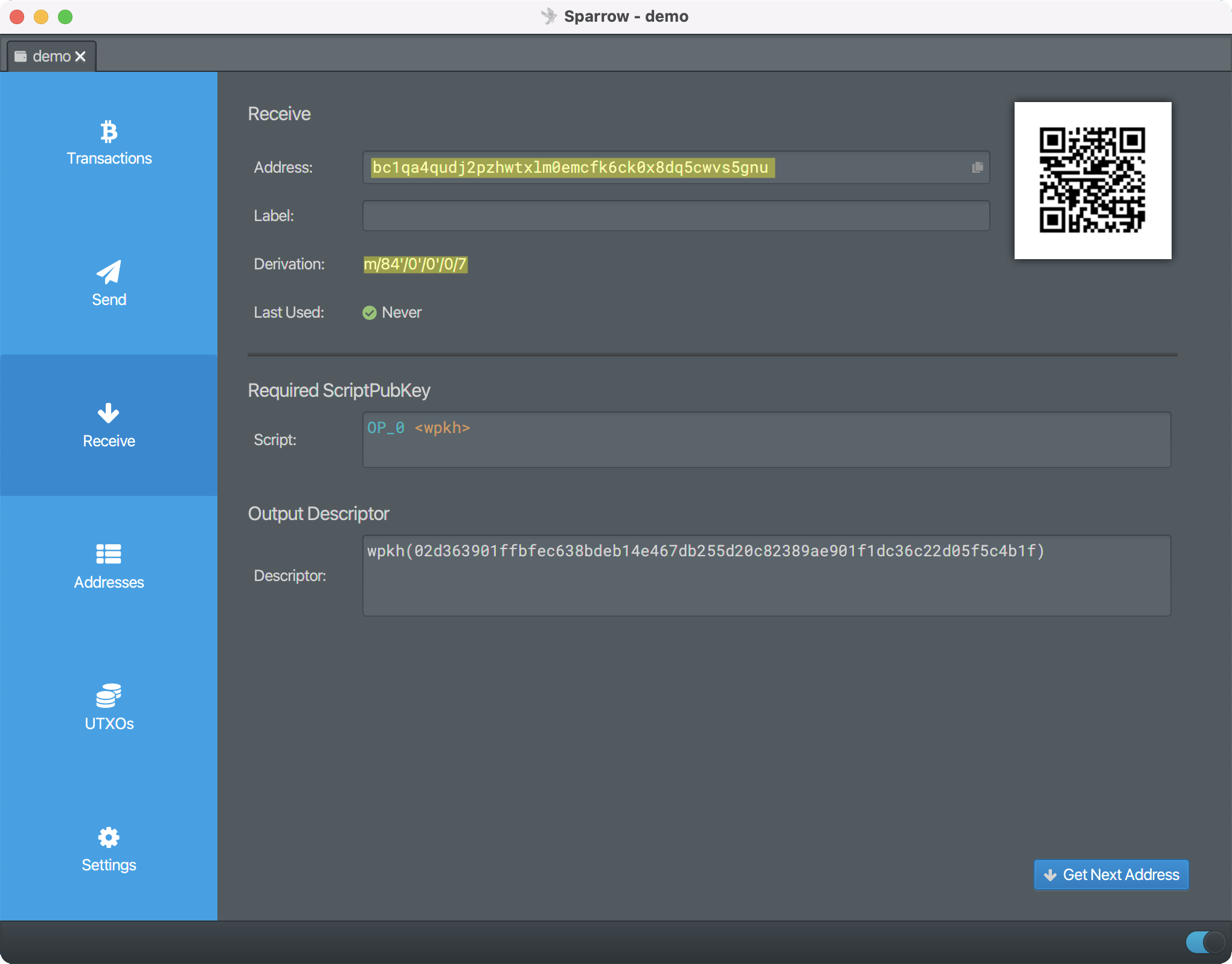
In the example above we see a specific address and its derivation, from
the derivation we can see that it is the 7th receiving
address of the 0th bitcoin account on the branch intended for
Native Segwit (P2WPKH) addresses. Note: I don't recommend using say the
100th receive address before using any of the addresses
before it as this will likely be greater than your wallets gap limit and
bitcoin sent to this address may not be shown and may cause headaches
when recovering funds.





