RSA Encryption
 Contents
Contents
- Keys
- Encryption
- Decryption
- Signing messages
- Python Implementation
Keys
Naturally, private keys are kept private and public keys are made
public.
Private key = (p,q) where p and q are primes
Public key = (N,e) where N = p*q and e = 65537
Encryption
The message is converted to an integer, m. This integer m must be
smaller than N and ideally smaller than both p and q, it is converted to
ciphertext by the following:
Ciphertext,
c = me (mod N)
(See
modular arithmetic
for an explanation of the (mod N) notation.)
Decryption
To find m from c it suffices to find the multiplicative inverse of e
modulo φ(N) i.e. d such that e*d = 1 mod(φ(N)), where φ is
Euler's totient function. Then by
Euler's theorem
we have that:
cd = me*d = mk*φ(m) + 1 =
(mk)φ(N)*m = m mod(N)
(Since e*d = k*φ(m) + 1 for some integer k.)
Conveniently, φ(N) is easy to calculate if you know the prime
decomposition of N but very hard to calculate for large N if you do not
know the prime decomposition of N, and factoring N is very hard when N
is the product of two very large prime numbers.
φ(N) = (p-1)*(q-1) = N - (p+q) + 1
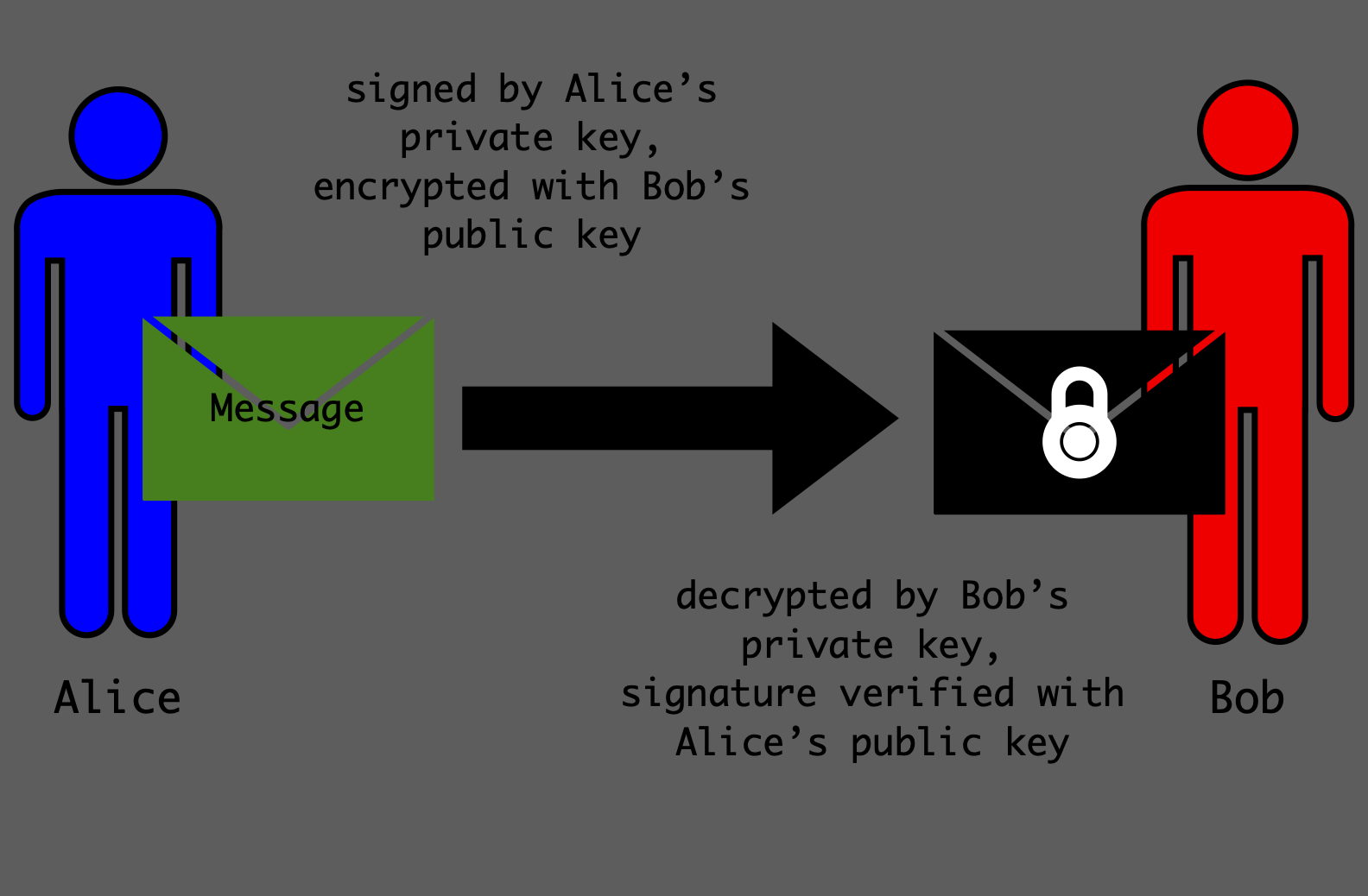
Signing messages
Let h be the
hash
of the message.
h = hash(message)
The signature is the integer s,
s = hd mod(N)
Where d is the multiplicative inverse of e modulo φ(N) as in the
decryption section above. Thus only the owner of a private key can
produce a valid signature butanyone can verify the validity of this
signature by confirming that se = h mod(N) since again by
Euler's theorem:
se = (hd)e = hd*e = he*d
= h mod(N)
Thus proving that the message is from the owner of the private key
corresponding to the public key (N,e) and that the message has not been
tampered with.
Python Implementation
Check out
this
implementation I wrote in Python with a gui made with
tkinter.
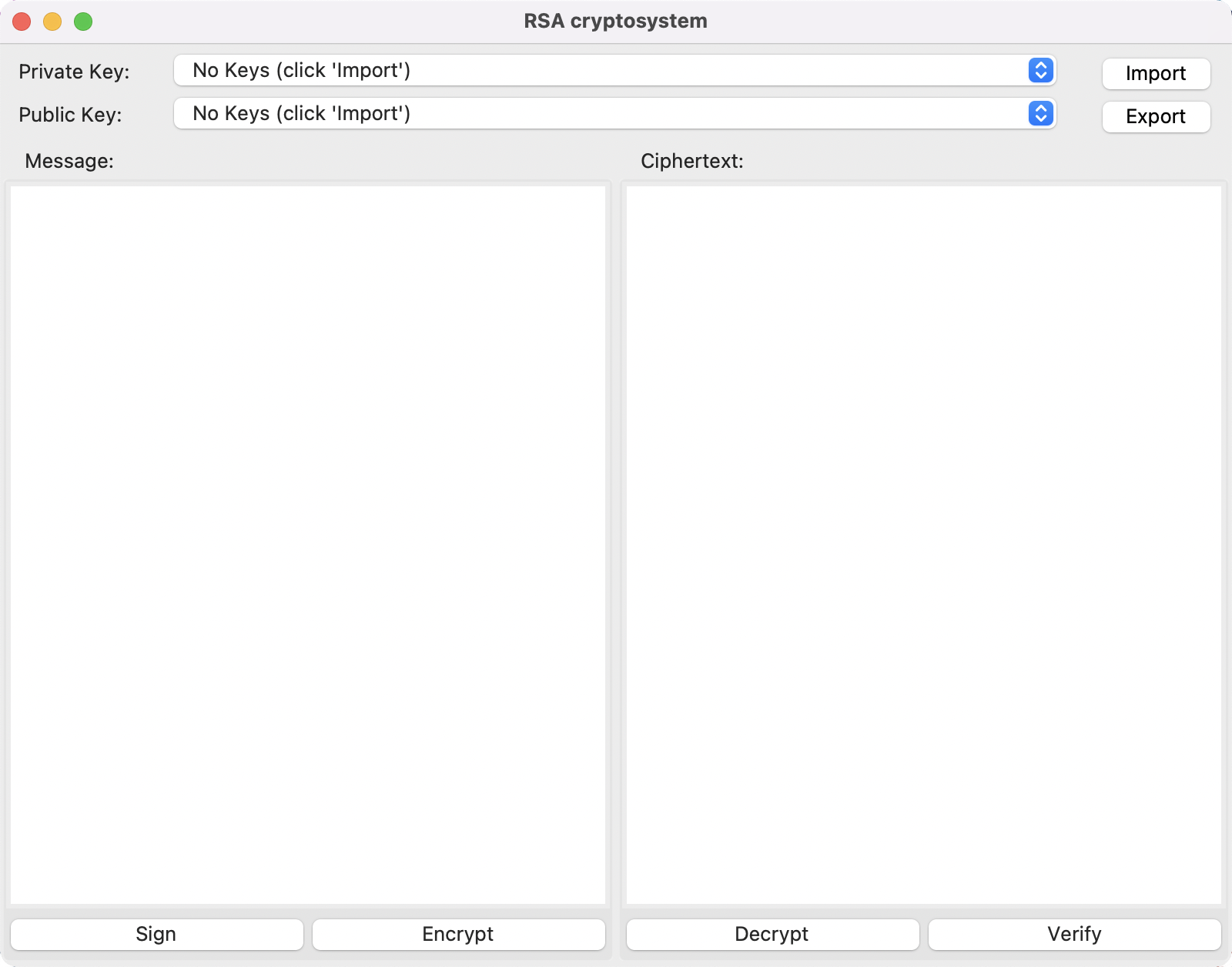
Try sending an encrypted message to me (via any method in the footer),
my public key is:
pubkey_tWRbnJAvBRQWmEsSv5Ly3Fh7Mxqy0N5ZeJX3WsKryNHX2LVSdeLGsd2lZMMSuNmAWkROGio7fU9jOYvCYqL2VitOaqGXlgD2Ym0z6OhB9MeFjpJOp3gt9yYDHFqaf9iQTJEYFBgrDsuQCMlKPq4U7gkCnR6eYftELYm9nPBFoYWT_h33_
(Note: keys and ciphertext are represented in base 62 (i.e. using
symbols 0-9, a-z and A-Z) instead of the usual base 10 for the sake of
brevity.)

